Branch and bound search is used in optimisation situations for tree seadch or {graph search when there is a cost associated with the path taken to reach a solution, and we want to find the solution with the least path cost. The path cost is often additive, for example minimising the number of moves to get to a solution, distances between locations along a geographic route, where each move in a puzzle has a cost. However, branch and bound search does not rely on this, merely that the costs of a path are monotonic, that isnthey increase if the path gets longer. The key insight of branch and bound search is that once we have found best-yet solution, we can prune whole branches for which the path to the branch node exceeds the current best solution. In addition, the path cost to a node can be used as a heuristic to order the open list and choose which nodes to explore first.
Defined on page 69
Used on pages 69, 70, 92, 224
Also known as branch and bound
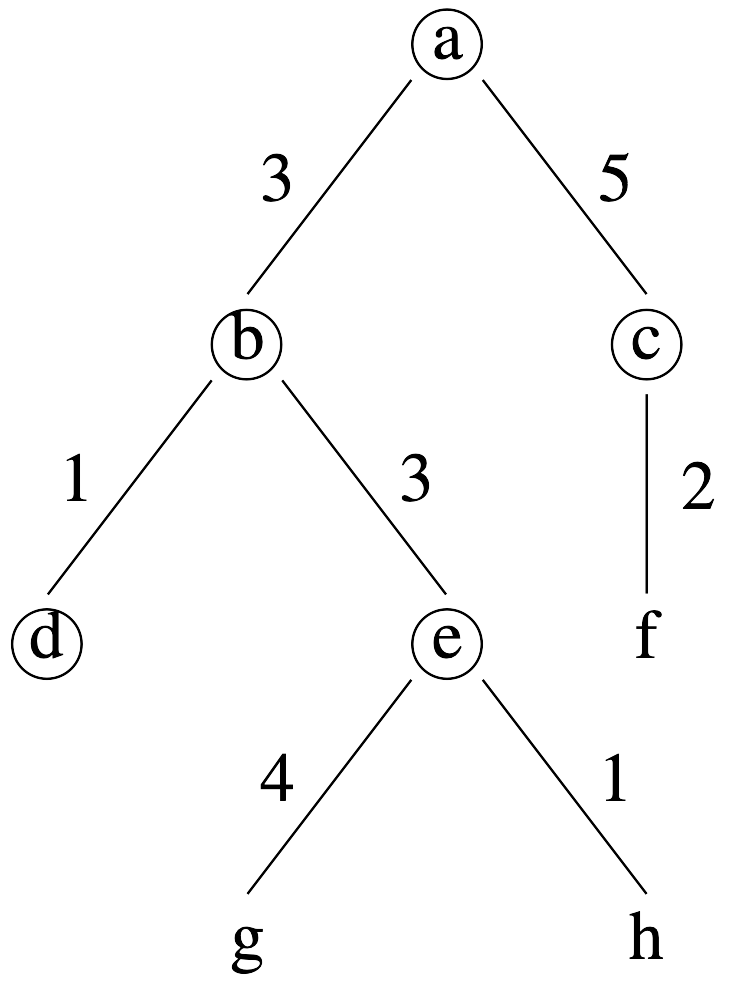
Search tree with path costs